4º Matemáticas

MATEMÁTICAS

PRIMER TRIMESTRE

TEMA 1: NUMERACIÓN

·         Números de cinco cifras

Los números de cinco cifras están formados por:

-        Unidades: 23.548

-        Decenas:  23.548

-        Centenas:  23.548

-        Unidades de millar: 23.548

-        Decenas de millar: 23.458

¿Cómo leemos estos números?

1.  23

Leemos el número que hay antes del punto:

Veintitrés

2.      .458
Leemos el punto.

        23 . 458

            Veintitrés mil

3.      Leemos el segundo número después del punto.

23. 458

            Veintitrés mil cuatrocientos cincuenta y ocho.

Recuerda que tenemos que descomponer los números de las dos maneras, por su valor de posición y por la posición de la cifra dentro del número:

        23.548:           2 D.M; 3 U.M; 5 c; 4 d; 8 u

20.000 u; 3.000u; 500c; 40d; 8u

 Los números de seis cifras están formados por:

-        Unidades: 23.548

-        Decenas:  23.548

-        Centenas:  23.548

-        Unidades de millar: 23.548

-        Decenas de millar: 23.458

-        Centenas de millar: 623.458

¿Cómo leemos estos números?

1 . 623

Leemos el número que hay antes del punto:

 Seiscientos veintitrés

Leemos el punto.

        623  .  458

            Seiscientos veintitrés mil

3.      Leemos el segundo número después del punto.

 

            Seiscientos veintitrés mil cuatrocientos cincuenta y ocho.

Recuerda que tenemos que descomponer los números de las dos maneras, por su valor de posición y por la posición de la cifra dentro del número:

        623.548: 6 C.M;      2 D.M;   3 U.M;   5 c;      4 d;    8 u

              600.000u; 20.000u; 3.000u;   500c;   40d;   8u

Los números de siete cifras están formados por:

-        Unidades: 23.548

-        Decenas:  23.548

-        Centenas:  23.548

-        Unidades de millar: 23.548

-        Decenas de millar: 23.458

-        Centenas de millar: 623.458

-        Unidades de millón: 7.623.458

¿Cómo leemos estos números?

1.     

623

Leemos el número que hay antes del primer  punto:

                7                  .458

            Siete

2.     

.

Leemos el punto.

            7              623. 458

            Siete millones

3.      Leemos el segundo número después del primer punto.

623.

7.                    458

            Siete millones seiscientos veintitrés

4.     

.

Leemos el siguiente punto.

7. 623            458

 Siete millones seiscientos veintitrés mil

5.      Leemos el número después del punto.

458

7.      623.   .

Siete millones seiscientos veintitrés mil cuatrocientos cincuenta y ocho.

Recuerda que tenemos que descomponer los números de las dos maneras, por su valor de posición y por la posición de la cifra dentro del número:

        7. 623.548: 7 U.M 6 C.M;      2 D.M;   3 U.M;            5 c;      4 d;    8 u

              7.000.000u;  600.000u; 20.000u; 3.000u;   500c;   40d;   8u

·         Aquí tienes unas cuantas actividades para practicar estos contenidos:

http://www.ceipjuanherreraalcausa.es/Recursosdidacticos/CUARTO/Matematicas/datos/U01/01.htm

http://www.genmagic.net/mates4/sermat1c.swf escribir numeros

http://www.educa.jcyl.es/educacyl/cm/zonaalumnos/tkPopUp?pgseed=1191353120911&idContent=20739&locale=es_ES&textOnly=false

http://www.educa.jcyl.es/educacyl/cm/zonaalumnos/tkPopUp?pgseed=1191353120911&idContent=20739&locale=es_ES&textOnly=false dictado numérico

http://www.educa.jcyl.es/educacyl/cm/zonaalumnos/tkPopUp?pgseed=1191353120911&idContent=20739&locale=es_ES&textOnly=false  series

http://www.juntadeandalucia.es/averroes/carambolo/WEB%20JCLIC2/Agrega/Matematicas/Aproximacion%20en%20el%20calculo/contenido/index.html aproximaciones.

http://www.genmagic.net/repositorio/thumbnails.php?album=search&search=valor_posicional valor de posición

SEGUNDO TRIMESTRE

TEMA 6: LAS FRACCIONES

·         ¿Qué es una fracción? El concepto  de fracción corresponde a la idea de dividir una totalidad en partes iguales, como cuando hablamos, por ejemplo, de un cuarto de hora, de la mitad de un pastel, o de las dos terceras partes de un depósito de gasolina. Tres cuartos de hora no son, evidentemente, la misma cosa que las tres cuartas partes de un pastel, pero se “calculan” de la misma manera: dividiendo la totalidad (una hora, o el pastel) en cuatro partes iguales y tomando luego tres de esas partes.

1.Aquí repasarás y jugarás con lo que hemos estudiado en el cole: http://www.wikisaber.es/Contenidos/LObjects/common_frac/launch.html

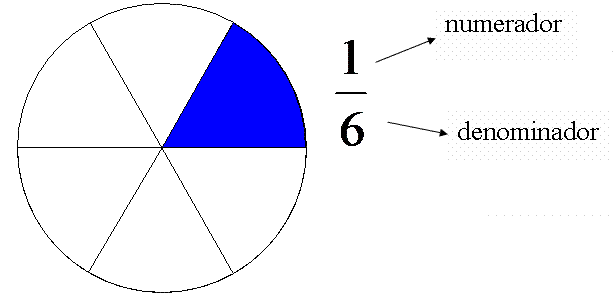
·     ¿Cómo se escribe una fracción? Una fracción se representa matemáticamente por números que están escritos uno sobre otro y que están separados por una línea recta horizontal llamada raya fraccionaria.  

5

6

2.Sigue practicando la fracción: 

http://www.juntadeandalucia.es/averroes/carambolo/WEB%20JCLIC2/Agrega/Matematicas/Fraccion_y_numero_decimal-CONTENIDOS/contenido/mt10_oa01_es/index.html

·         Términos de una fracción: La fracción está formada por dos términos: el numerador y el denominador. El numerador es el número que está sobre la raya fraccionaria y el denominador es el que está bajo la raya fraccionaria.

TÉRMINOS DE UNA FRACCIÓN

5	Numerador
—	-
6	Denominador

3.      Aquí encontrarás más ejercicios: 

http://www.gobiernodecanarias.org/educacion/3/WebC/eltanque/todo_mate/fracciones_e/ejercicios/fraccionesej10_p.html

 

·         ¿Qué es el numerador? El Numerador indica el número de partes iguales que se han cogido de una parte entera.

·         ¿Qué es el denominador? El Denominador indica el número de partes iguales en que se ha dividido una parte  entera.

·         ¿Cómo se lee? Por ejemplo, la fracción 3 / 4 (se lee tres cuartos) tiene como numerador al 3 y como denominador al 4. El 3 significa que se han cogido 3 partes de una parte entera  de 4 partes en que se dividió el entero o el todo.

·         Cuando comparamos dos fracciones con el mismo denominador es mayor la que tiene mayor el numerador.

4.      Atrévete a seguir comparando todas estas fracciones: 

http://cerezo.pntic.mec.es/maria8/bimates/operaciones/fracciones/concepto.html

5.      Sigue practicando la comparación: 

http://www.vedoque.com/juegos/matematicas-04-fracciones.swf?idioma=es

6.      http://ntic.educacion.es/w3//recursos/primaria/matematicas/fracciones/menuu2.html

·         ¿Cómo se calcula la fracción de un número? Primero dividimos ese número por el denominador de la fracción y después multiplicamos el resultado por el numerador.

4 de 21               21: 7= 3

7                         3 x 4= 12

7.      Aquí practicarás  para aprender más: 

http://www.gobiernodecanarias.org/educacion/3/WebC/eltanque/todo_mate/fracnum/fracnum_p.html

Ejemplos:

Hay 8 partes de las cuales se han pintado 5, por lo tanto, la fracción que representa matemáticamente este dibujo es 5 / 8 (se lee cinco octavos).

Hay 3 partes pintadas de un total de 5. Esto se representa como 3  / 5 (se lee tres quintos)

TEMA 7: NÚMEROS DECIMALES

·         ¿Qué es un número decimal? Es un número que nos dice que tenemos una parte que es entera, por ejemplo 3, y otra parte que es decimal es decir no es entera y pertenece al siguiente número entero, por ejemplo  3, 7 (en este número tenemos tres partes enteras y 7 partes decimales)

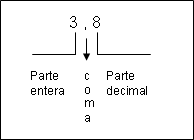
·         Partes de un número decimal:  El número decimal tiene dos partes: entera y decimal. EN el número 3,7 el tres es la parte entera y el siete es la parte decimal.

·         Valor de posición del número decimal:  En la parte decimal hablamos de décimas y centésimas. Una décima es dividir una parte en 10 partes iguales:

1 unidad = 10 décimas = 1  = 0,1 unidades

                                                10

Una centésima es dividir una parte en cien partes iguales:

1 unidad= 100 centésimas =      1  = 0,01 unidades

                                                         100

·         Para leer un número decimal primero leemos la parte entera y después la parte decimal si es con décimas decimos décimas y si es con centésimas acabamos diciendo centésimas.

 Por ejemplo: 3, 7                           tres coma siete

                                                              Tres unidades y siete décimas

                        3, 74                             tres coma setena y cuatro

                        3, 74                             tres unidades y setenta y cuatro              centésimas

·         ¿Cómo comparamos un número decimal? Primero comparamos la parte entera, si la parte entera es igual empezamos a comparar la parte decimal empezando por las décimas y siguiendo por las centésimas.

1.       Atrévete con este mega trivial de números decimales: 

http://www.testeando.es/test.asp?idA=66&idT=omyqvywc

2.       

Ahora lee bien estos números: 

http://www.gobiernodecanarias.org/educacion/3/WebC/eltanque/todo_mate/decimales_e1/comoseleen_p.html

3.       

Si resuelves todo el crucigrama eres un crack: 

http://www.educa.jcyl.es/educacyl/cm/zonaalumnos/tkPopUp?pgseed=1168680284242&idContent=20742&locale=es_ES&textOnly=false

4.       A comparar números decimales: 

http://www.gobiernodecanarias.org/educacion/3/WebC/eltanque/pizarradigital/NumDec5/mas_actividades/menor/Menor_que.html

5.       Sigue comparando: 

http://cplosangeles.juntaextremadura.net/web/edilim/curso_4/matematicas/decimales_4/decimales_4.html

6.       Repasa las décimas: 

http://www.gobiernodecanarias.org/educacion/3/WebC/eltanque/pizarradigital/NumDec5/decimas/decimas_5_p.html

7.       Más décimas: 

http://ntic.educacion.es/w3/recursos/primaria/matematicas/decimales/menuu1.html

8.       Ahora a por las centésimas

 http://ntic.educacion.es/w3/recursos/primaria/matematicas/decimales/menuu1.html

9.       Con esto sabes mucho de números decimales: 

http://www.gobiernodecanarias.org/educacion/3/WebC/eltanque/pizarradigital/NumDec5/centesimas/centesimas_5cubo_p.html

TEMA 8: OPERACIONES CON DECIMALES

·         Recuerda que todo lo relacionado con el euro lo tienes dentro del blog en la pestaña de matemáticas de tercero.

·         ¿Cómo se suma y se restan números decimales? Se opera igual que con los números enteros. Tenemos que colocar perfectamente los números, centésimas con centésimas, décimas con décimas y la parte decimal con la parte decimal.

    4  3  2, 8  4

+ 5  4   6, 6  7

    9  7  9, 5   1

1.       Empieza con estas operaciones: 

http://www.gobiernodecanarias.org/educacion/3/WebC/eltanque/todo_mate/sumayresta_d/ocd_p.html

2.       

Venga ahora atrévete con estas algo más difíciles: 

http://www.gobiernodecanarias.org/educacion/3/WebC/eltanque/todo_mate/openumdec/resta_dec/resta_dec.html

3.       

Vamos subiendo la dificultad de las operaciones: 

http://www.genmagic.net/repositorio/albums/userpics/ompcel1c.swf

4.       Aprovecha estos juegos para operar con euros: 

http://www.educa.jcyl.es/educacyl/cm/zonaalumnos/tkPopUp?pgseed=1168680284242&idContent=20742&locale=es_ES&textOnly=false

5.       Venga que ya va quedando menos: 

http://ntic.educacion.es/w3/recursos/primaria/matematicas/decimales/menuu5.html

6.       Cuidado con estos bloques: 

http://nlvm.usu.edu/es/nav/frames_asid_264_g_1_t_1.html?from=topic_t_1.html

7.       Y para terminar un repaso y unas operaciones: 

http://ntic.educacion.es/w3//eos/MaterialesEducativos/mem2008/visualizador_decimales/suma_resta_decimales.html

TEMA 9: MEDIDA DE LONGITUDES

·         Recuerda que la unidad principal de longitud es el metro al que representamos con la letra m

·         Tenemos unidades de medida más pequeñas que el metro para medir objetos o distancias pequeños:

Þ      1m = 10 dm

Þ      1m = 100 cm

Þ      1m = 1000 mm

Þ      1m = 10dm = 100cm = 1000mm

·         También tenemos unidades de medida más grandes que el metro para medir objetos o distancias mayores:

Þ      1 dam = 10 m

Þ      1 hm   =  100 m

Þ      1 km   =  1000 m

Þ      1km = 10 hm = 100 dam = 1000 m

·         Acuérdate que para operar con unidades de medida tenemos que tenerlas expresadas en la misma unidad, es decir, puedo sumar centímetros con centímetros  pero no puedo operar centímetros con decímetros. Antes de hacer la operación tengo que pasarlo a la misma unidad.

1.       Para empezar medimos algunos objetos:

 http://www.ucoerm.net/public/medimos.swf

2.       Juega con las unidades más pequeñas que el metro: 

http://www.genmagic.org/repositorio/albums/userpics/tequi2c.swf

3.       Aquí puedes repasar todo lo anterior: 

http://cerezo.pntic.mec.es/maria8/bimates/medidas/longitud/unidades.html

4.       Atrévete a ayudar a este pobre explorador perdido: 

http://www.juntadeandalucia.es/averroes/carambolo/WEB%20JCLIC2/Agrega/Matematicas/Longitud/contenido/ma015_oa01_es/index.html

5.       Ahora a por estas tablas de equivalencia: 

http://genmagic.net/repositorio/albums/userpics/tequi1c.swf

6.       A por estas relaciones entre unidades de medida: 

http://www.gobiernodecanarias.org/educacion/3/WebC/eltanque/todo_mate/r_medidas/longitud_p.html

7.       Repasa todo lo que hemos aprendido 

http://www.juntadeandalucia.es/averroes/~cepgr2gt1/intranet4/mat/longitud/longitud.htm

8.       A por el nivel dificiliiiiiiiiiiiiiiiiiiiiiiiiiisimo 

http://www.educa.jcyl.es/educacyl/cm/zonaalumnos/tkPopUp?pgseed=1168680284242&idContent=20742&locale=es_ES&textOnly=false

TERCER TRIMESTRE

TEMA 10

TEMA 11

TEMA 12

TEMA 13

TEMA 14

TEMA 15